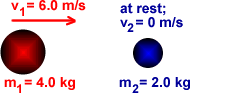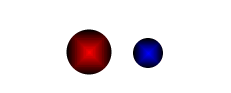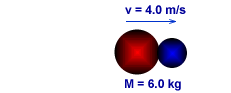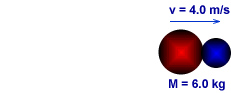
In an inelastic collision, two (or sometimes more, but let's not get carried away) objects collide and stick together. We generally ignore any outside forces on the colliding objects, so the two-object system is an isolated system. This is reasonable in practice if we examine the objects during the time interval immediately before the collision and then immediately after - before friction, gravity, etc., have time to exert any appreciable impulses on our system.
| An Inelastic Collision |
|---|
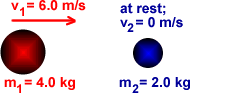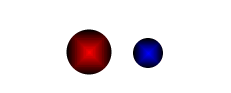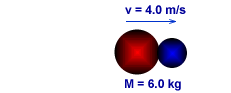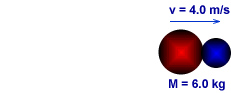 |
The standard method for handling inelastic collisions in one dimension is to invoke the Law of Conservation of Momentum. After all, if no external forces act on a system, its total momentum will be conserved.
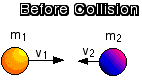 |
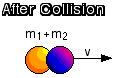 |
|
Total momentum of the system (the two objects) before the collision is: |
Total momentum of the system after the collision: |
If momentum is conserved, then:
pafter = pbefore
so that:
(m1 + m2)v = m1v1 + m2v2
Solving for v gives:
Look! Wait a minute! This is just the velocity of the center of mass of the system! Of course! Since no external forces act on the system, its center of mass does not accelerate (Newton's First Law)! (Here's a QuickTime simulation.) The fact that the velocity of the center of mass is constant generally provides a quick and straightforward solution for inelastic collision problems.
| The System's Center of Mass Has a Constant Velocity During an Inelastic Collision! |
|---|
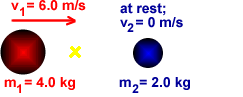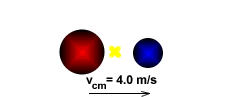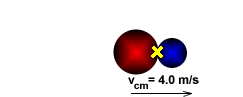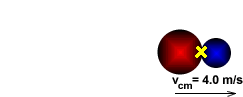 |
A 4.0-kg meatball is moving with a speed of 6.0 m/s directly toward a 2.0 kg meatball which is at rest. The two meatballs collide and stick together. What is their velocity immediately after the (inelastic) collision?

Since no external forces act on the two-meatball system, its center of mass does not accelerate. In other words, the velocity of the center of mass after the collision is the same as the velocity of the center of mass before the collision, and the velocity of the center of mass before the collision is easy to calculate:
Since the two meatballs must be moving with the center of mass after the collision, their velocity must be 4.0 m/s after the collision.
Here is an alternate solution using conservation of momentum - a more-traditional approach.
Having both colliding objects moving before the collision introduces no major complications (just one additional term to deal with) to the solution, as shown below.
Two meatballs are speeding directly toward each other. One is a 4.0-kg meatball moving with a speed of 6.0 m/s, and the other has a mass of 2.0 kg and a speed of 4 m/s. If they collide inelastically, what will be the speed of the resulting 6.0 kg meatball immediately after the collision?

Since the center of mass of the two-meatball system does not accelerate, the velocity of the 6.0 kg meatball after the collision equals the velocity of the system's center of mass before the collision:
The velocity of the 6.0-kg meatball will be about 2.7 m/s immediately after the collision.
Here is an alternate solution using Conservation of Momentum - a more traditional approach.
A bullet with a mass of 0.020 kg collides inelastically with a wooden block of mass 2.5 kg, initially at rest. After the collision, the bullet + block has a speed of 1.2 m/s. What was the initial speed of the bullet?

This problem is essentially the same as Example 1. Since no external forces act on the system, the velocity of the center of mass of the bullet + block system remains constant. Therefore, the velocity of the center of mass of the system is 1.2 m/s, the velocity of the bullet + block after the collision. If v1 = the velocity of the bullet, and v2 = the initial velocity of the block ( = 0 m/s), then:
The speed of the bullet just before it hit the block was about 150 m/s.
Here is an alternate solution that uses Conservation of Momentum - a more-traditional approach.
last update March 21, 2006 by JL Stanbrough