Conceptual:
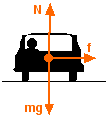 Suppose
the car is going around an unbanked (level) curve (as in the
diagram on the previous page). The
diagram at left shows a free-body diagram of the forces
acting on the car.
Suppose
the car is going around an unbanked (level) curve (as in the
diagram on the previous page). The
diagram at left shows a free-body diagram of the forces
acting on the car.
The downward force labeled "mg" is the weight of the car (the Earth pulling downward on the car). The upward force, labeled "N" (for "Normal") is the force the road exerts on the car perpendicular to the surface of the road. We know that the car is not accelerating vertically, so Newton's First Law tells us that these two forces must cancel exactly, so that the vertical net force on the car is zero.
We know that there must be a horizontal net force on the car, however - the centripetal force. In the diagram, the horizontal force labeled "f" represents the horizontal friction force that the road exerts on the car's tires. This force must be the centripetal force! This friction force points toward the center of the turn, and is responsible for turning the car.
So, in an unbanked turn, the force responsible for turning the car is the friction force between the tires and the road. To see how this works, think of what would happen if there were no friction. Have you ever found yourself driving on ice? The car doesn't want to turn because there is little or no friction between the ice-covered road and the car's tires. Usually you are too panicked at the time to notice, but you slide straight ahead into the ditch!
Another very important feature of this diagram is there is NO outward-pointing force! The friction force points inward - toward the center of the turn (circle). Yes, you feel "thrown outward," but this is due to your inertia. There is no centrifugal force!
From the free-body diagram above and Newton's Second Law we can write:
N = mg (vertical forces cancel)Fnet = Fcentripetal = f (horizontal net force)
Remember that Fcentripetal = mv2/r and the
friction force, ![]() ,
and you've got it.
,
and you've got it.
A 1000 kg car is going around a curve with radius 30 meters. If the coefficient of friction between the car's tires and the road is 0.5, what is the maximum speed at which the car can make the turn?

In the vertical direction, N = mg. In the horizontal direction:
Fnet = Fcentripetal = f
The maximum velocity for the car is about 12 m/s. Notice that the mass of the car doesn't matter - it drops out of the equation in step 3. It doesn't matter if you are driving a Hummer or a Hugo (well, at least as far as the physics of turning, anyway...), the maximum speed on this curve will be 12 m/s for any vehicle with the same coefficient of friction.
Examine the equation ![]() .
This equation says that your speed on a curve is proportional to the
square root of the coefficient of friction between your tires and the
road,
.
This equation says that your speed on a curve is proportional to the
square root of the coefficient of friction between your tires and the
road, ![]() .
If
.
If ![]() is four times as much, your maximum speed doubles. If
is four times as much, your maximum speed doubles. If ![]() = 0, you aren't going to make it (see above)!
This makes sense.
= 0, you aren't going to make it (see above)!
This makes sense.
The equation ![]() also says that your maximum speed is proportional to the square root
of the radius of the curve - you could go about 1.4 times as fast on
a curve with a 60 meter (twice as much) radius.
also says that your maximum speed is proportional to the square root
of the radius of the curve - you could go about 1.4 times as fast on
a curve with a 60 meter (twice as much) radius.
What about the effect of "g"? Will highways on the Moon be faster or slower than highways on Earth?
Suppose that the coefficient of friction between a typical tire and a particular highway surface is 0.75. What should be the minimum radius for curves on this highway if the speed limit is 55 miles per hour?

In the vertical direction, N = mg. In the horizontal direction:
Fnet = Fcentripetal = f
The minimum radius for curves on this highway is about 270 ft.
First, notice that the setup for this problem is the same as for example 1 - it's all the same physics, only the algebra is different. Also, notice how the conversion factors are used in the second-to-last step to convert mi/hr to ft/sec.
Have a look at the equation ![]() .
Since r is proportional to the square of v, it predicts that doubling
the speed will require a curve of four times the radius.
.
Since r is proportional to the square of v, it predicts that doubling
the speed will require a curve of four times the radius.