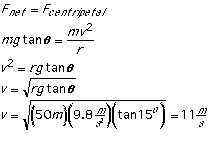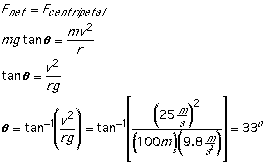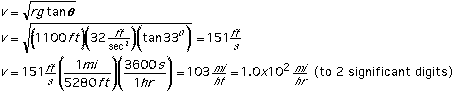A Banked Turn - No Friction





What if there is absolutely no friction between a car's tires and the
road - could the car still get around a curve? Well, yes, it
could happen if the curve is banked, and
the car had precisely the right speed. Here's how:
Conceptual:
|
|
|
|
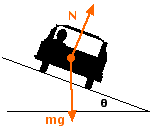
A Car on a Level Surface
All forces on the car are vertical, so no horizontal
force can be generated.
|
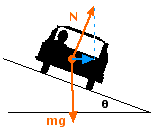
A Car on a Banked Turn
The normal force on the car due to the road is no longer
vertical, so a component of the normal force acts in the
horizontal direction.
|
The Centripetal Force
The horizontal component of the normal force is shown in
blue in the diagram above. This force can supply a
centripetal force to turn the car.
|
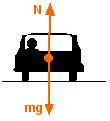
If a car is on a level (unbanked) surface, the forces acting on the
car are its weight, mg, pulling the car downward, and the normal
force, N, due to the road, which pushes the car upward. Both of these
forces act in the vertical direction and have no horizontal
component. If there is no friction, there is no force that can supply
the centripetal force required to make the car move in a circular
path - there is no way that the car can turn.
On the other hand, if the car is on a banked turn, the normal
force (which is always perpendicular to the road's surface) is no
longer vertical. The normal force now has a horizontal component, and
this component can act as the centripetal force on the car! The car
will have to move with just the right speed so that it needs a
centripetal force equal to this available force, but it could be
done. Given just the right speed, a car could safely negotiate a
banked curve even if the road is covered with perfectly smooth
ice!
Mathematical:
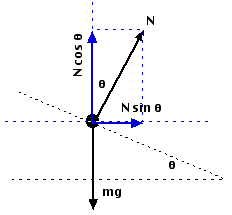 A
free-body diagram for the car on the banked turn is shown at left.
The banking angle between the road and the horizontal is
A
free-body diagram for the car on the banked turn is shown at left.
The banking angle between the road and the horizontal is 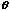 (theta). The normal force, N, has been resolved into horizontal and
vertical components (the blue vectors).
(theta). The normal force, N, has been resolved into horizontal and
vertical components (the blue vectors).
In the vertical direction there is no acceleration, and:
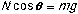
so:
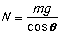
In the horizontal direction:
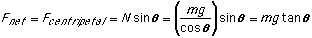
Since Fnet = Fcentripetal:
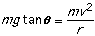
Solving for v gives:
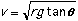
A car moving at velocity v will successfully round the curve!
Note: Your initial thought might have been to resolve the
weight vector parallel and perpendicular to the road - after all,
that is what we did for all of those lovely inclined plane problems,
remember? The difference is that we expected the object to accelerate
parallel to the incline, so it made sense to have the vectors
pointing parallel and perpendicular to the incline. Here, though, the
acceleration is horizontal - toward the center of the car's circular
path - so it makes sense to resolve the vectors horizontally and
vertically.
Example 1:
A curve has a radius of 50 meters and a banking angle of
15o. What is the ideal, or critical, speed (the speed for
which no friction is required between the car's tires and the
surface) for a car on this curve?
Solution:

- radius of curve, r = 50 m
- banking angle,
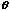 = 15o
= 15o
- free-fall acceleration, g = 9.8 m/s2
- no friction speed, v = ?
From the free-body diagram for the car:
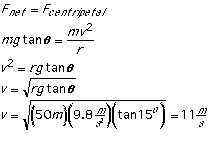
If the car has a speed of about 11 m/s, it can negotiate the curve
without any friction.
Example 2:
A turn of radius 100 m is being designed for a speed of 25
m/s. At what angle should the turn be banked?
Solution:

- radius of turn, r = 100 m
- speed of car, v = 25 m/s
- free-fall acceleration, g = 9.8 m/s2
- bank angle,
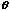 = ?
= ?
From the free-body diagram for the car:
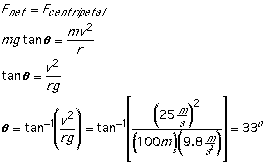
So, the banking angle should be about 33o. Whoops!
That's a pretty extreme angle, even for a race track (see example
3).
Example 3:
Talladega Motor Speedway in Alabama has turns with radius 1,100
ft. that are banked at 33o (source).
What is the "no friction" speed for a car on these turns?
Solution:
We can use the free-body diagram and derivation from example
1, and get:
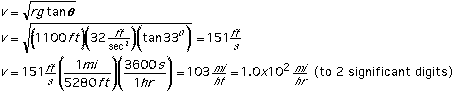
So, a car going about 100 mph could negotiate the turns at
Talladega without any friction between its tires and the pavement.
During a NASCAR race, however, the cars go through the turns at about
twice that speed...





last update April 21, 2008 by JL
Stanbrough



 A
free-body diagram for the car on the banked turn is shown at left.
The banking angle between the road and the horizontal is
A
free-body diagram for the car on the banked turn is shown at left.
The banking angle between the road and the horizontal is