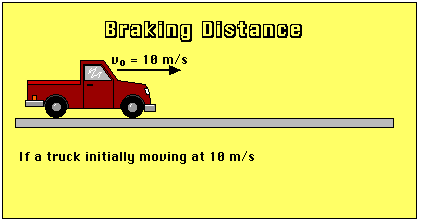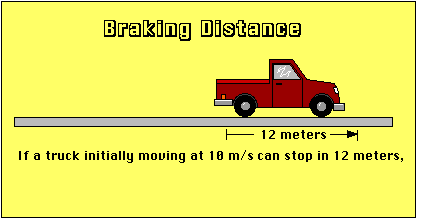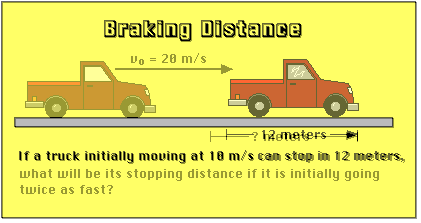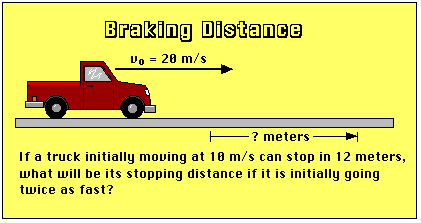

Here is some braking-distance data.
You might want to compare the following solution with the
|
Symbol |
Description |
Value 1 |
Value 2 |
|---|---|---|---|
|
|
Net braking force on the truck |
|
|
|
|
Braking distance of the truck |
|
|
|
|
Mass of the truck |
|
|
|
|
Final velocity of the truck |
|
|
|
|
Initial velocity of the truck |
|
|
In the table above, "Value 1" refers to the first situation, where the truck has a starting velocity of 10 m/s, and "Value 2" refers to the situation in which the truck has a starting velocity of 20 m/s. In both situations, we don't know what the braking force exerted on the truck is, but it would be a reasonable assumption that the force is the same in both situations. In the same way, we don't know what the mass of the truck is, but it shouldn't vary when the truck's velocity changes.
Solving the work-energy equation for the stopping distance gives:
(equation 1)
This shows that if Fnet and m are constant, then the car's stopping distance is directly proportional to the square of the starting velocity. (The term containing "v" disappears, since v = 0. Also, the negative sign indicates that Fnet and Æx are in opposite directions - if Fnet is negative, Æx will be positive, and vice versa.) This pretty-much tells you that if you double the velocity, you get four times the stopping distance, but if you need more convincing, we can use this result to write an expression for Æx10, the stopping distance when vo = 10 m/s:
The stopping distance for vo = 20 m/s is, therefore:
The numbers in this problem just get in the way - the problem can easily be solved for the general case. Doubling the initial velocity in equation 1 above gives:
So, doubling the velocity of the truck quadruples its stopping distance, regardless of the particular speeds involved.