Physics Simulation

Kinematics in One Dimension

BHS -> Staff -> Mr. Stanbrough -> AP Physics -> Kinematics -> this page

---

The Problem:

For example, given the following problem:

A car accelerates from rest at 4.0 m/s². How fast will it be going in 2.0 seconds, and how far will it have traveled?

---

The Simulation:

The only "trick" to simulating a kinematics problem like this in Interactive Physics^TM is that the program will not allow you to assign an object a particular acceleration, but there's an easy way around this (Newton's Second Law!). Here's how to set it up:

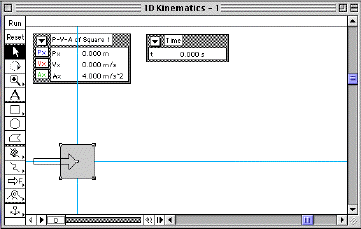
A screen shot of the simulation's main window

1. Preliminaries:
   1. Open the Interactive Physics^TM program.
   2. Turn on the xy-axes to help align your object.
   3. Turn off gravity.
2. Build the "car".
   1. Create a new object. It can be any shape. (It doesn't have to look like a car!)
   2. Open the object's Properties window, and set:
      1. x = 0.0 m
      2. y = 0.0 m
      3. v_x = 0.0 m/s
      4. v_y = 0.0 m/s
      5. mass = 1 kg. (Yes, I know that this makes a pretty small car, but don't worry about it...)
3. Build a force to accelerate the car.
   1. Create a new force with its arrow at the center of the object, pushing the object to the right.
   2. Open the force's Properties window, and set F_x = 4.0 N, and F_y = 0.0 N. (Notice that the force component F_x equals the desired acceleration - that's the "trick" - Newton's Second Law!)
4. Build the meters to measure the car's position and velocity.
   1. Create a P-V-A (Position-Velocity-Acceleration) meter for your object. You only need the X direction.
   2. Create a Time meter (clock).

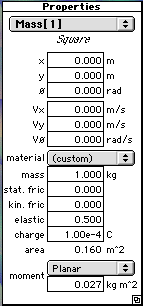
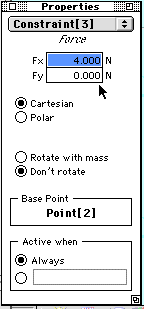
Properties window for the "car". You need new values for x, y, vx, vy, and mass.	Properties window for the force. You need to set values for Fx and Fy.

Now, run the simulation. Watch the timer, and stop after about 2.0 seconds. Don't worry if your object leaves the window - you don't need to see what it's doing. Also, you don't have to hit the stop time exactly, since you can use the "movie controls" at the bottom of the window to move the simulation a frame at a time till you find the one you want. You can read the simulations values for velocity and position after 2.0 seconds directly from the P-V-A meter. When I ran my simulation, I got v_x = 8.000 m/s, and p_x = 8.040 m.

---

Wait a minute!

The Simulation Accuracy dialog - with "Accurate" selected.

If a car accelerates from rest at 4.0 m/s², it will have a velocity of 4.0 m/s after 1.0 second, and 8.0 m/s after 2.0 seconds. (Its velocity changes by 4.0 m/s each second.) Its average velocity during this interval will be half of 8.0 m/s (the average of 0.0 m/s, its starting velocity, and 8.0 m/s, its ending velocity), which is 4.0 m/s. If a car has an average velocity of 4.0 m/s for 2.0 seconds, it should travel 8.0 m - not 8.04 m! What is going on here?

First, to be fair, notice that the position value is correct to 2 significant digits - it rounds to 8.0 m.

Secondly, you have to remember - when using any simulation - that it never calculates exact answers analytically. Instead, it uses a step-by-step incremental approach, and numerical errors will arise. So what do you do if you need more accuracy? In this case, it is sufficient to change the simulation's accuracy setting from "fast" to "accurate". Now, you get a final position of 8.000 meters. 

Any time you are going to use numerical results from Interactive Physics^TM, it is a good idea to make this switch to "Accurate". As you gain experience, you can use the "Custom" setting to check the validity of the results you get in the simulation by changing the time step and observing the effect on the results.

---

Add Some Vectors

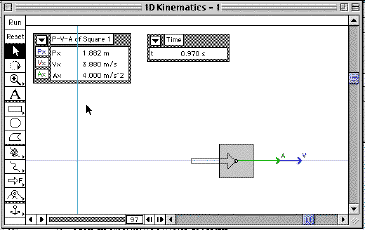
The simulation in progress with velocity and acceleration vectors added.

It would be a good idea to add velocity and acceleration vectors to the "car" so you can see how the change (or don't change) during the course of the simulation.

---

Some Additional Problems:

Modify your simulation to obtain solutions to the following problems. Then solve the problem analytically, if possible:

1. What will be the car's speed and distance traveled after 5.0 seconds?
2. If a car, initially at rest, has an acceleration of 2.0 m/s², how fast will it be going in 4.0 seconds? How far will it have traveled? (Hint: change F_x = 2.0 m/s².)
3. Suppose the car in the previous problem has a starting velocity of 10 m/s (instead of starting from rest). How fast will it be going in 2.0 seconds? How far will it travel in this time? (Hint: v_x = 10 m/s)
4. A car has a speed of 12 m/s when the brakes are applied. If the brakes can decelerate the car at 4 m/s², how far will the car travel before stopping, and how much time will it take to stop? (Hint: Reverse the force on the car by making F_x = -4.0 m/s². Watch the V_x meter.)
5. If the car in the previous problem has twice the speed when the brakes are applied (v_x = 24 m/s), how will this affect the stopping distance and stopping time?

---

[Lab Index]